Overview

The following tutorial will document how to program a keygenerator for diablo2oo2’s eighth crackme.

Functions and variables are labeled to make the tutorial easier to follow.

The crackme can be found here.

Reverse engineering the crackme.

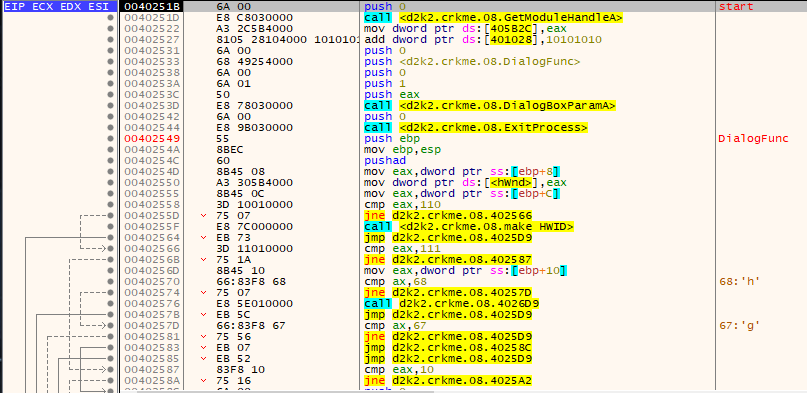
Load up the executable in x32dbg. The debugger should load the executable at the following code:

Run the crackme in x32dbg.

Immediately, there is some points of notice.

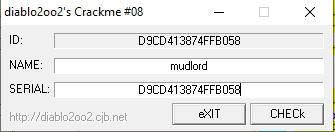
1. There is a “ID” being shown.
2. There is usage of bignum (arbitrary precision integer) library usage. This was determined by running the executable through the freeware version of IDA and using dihux’s “RESIG” FLIRT signature collection.

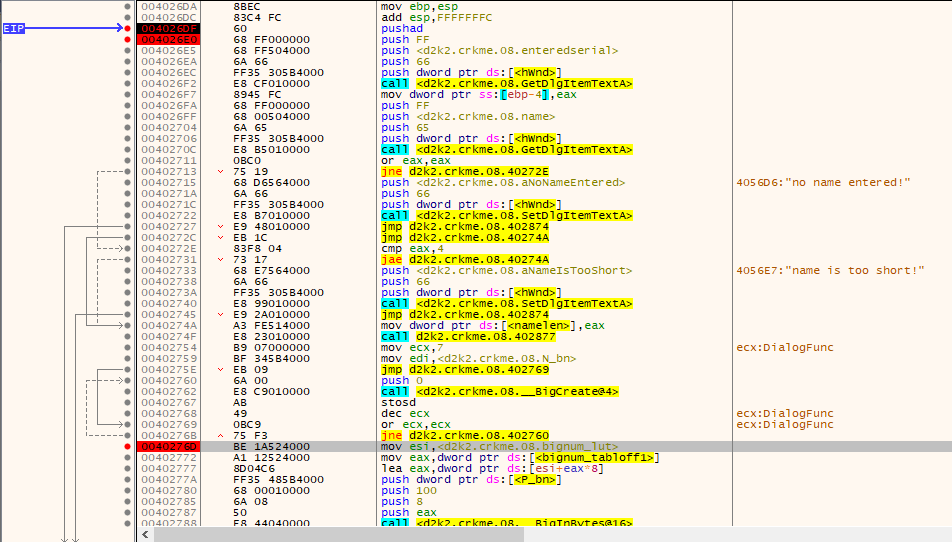
Place a breakpoint at 0x4026DF, enter any name into the name box (I used “mudlord”), enter a serial (I used the “ID shown”) and run…

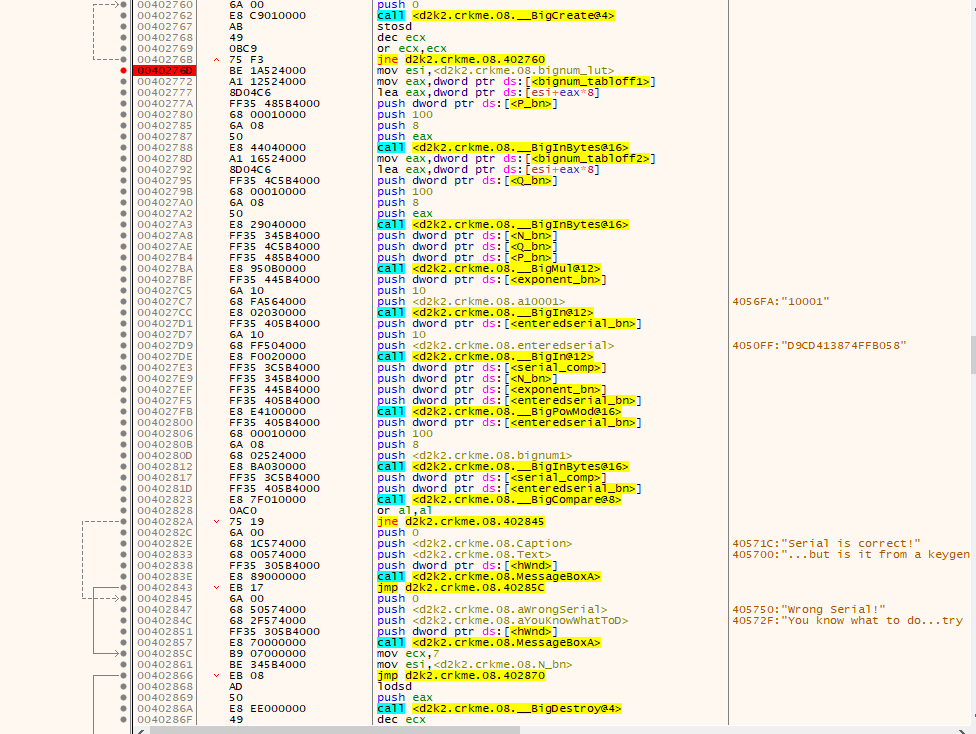
In this routine…..

• The username and serial are gathered
• Some results from earlier are somehow made into a bignum, in the function I labeled “makebignum”
• Some bignum variables are created
• Some bignums are initialized using data from a large table, using different variables to pick which portions of the table to use.
• 2 of these bignums are multiplied
• A bignum with something suspiciously like a RSA exponent (the “10001” value) is initialized
• A powmod operation is done (which is what used in RSA)
• The results from the powmod operation is checked with an entered serial which is converted into a bignum.

Clearly we need to find how the table is made, how the ID is made, and how the various portions of the table are picked.

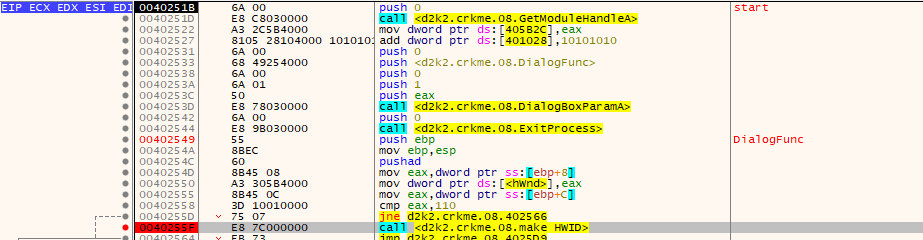
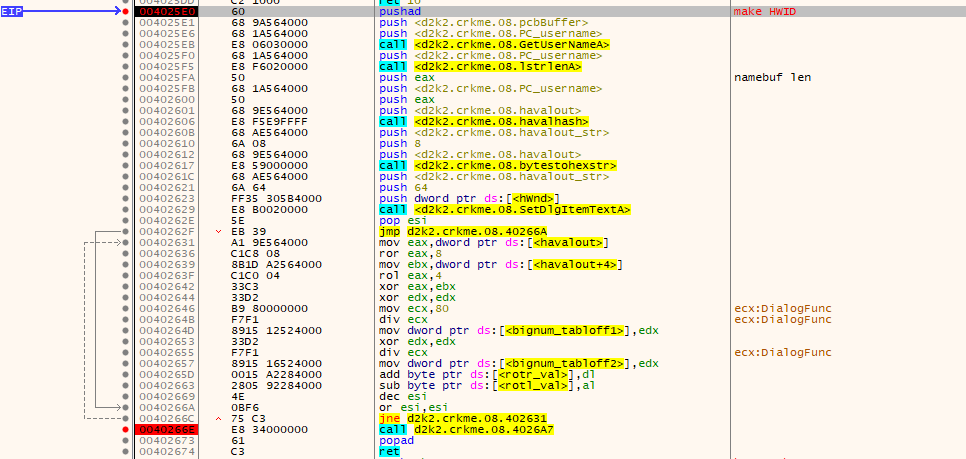
Restart the crackme and place a breakpoint on 0x0040255F.

Inside this function, which I labeled “make HWID”, various things happen.

• The computer’s username is retrieved.
• The computer username is hashed using a hash function, which I later determined to be derived from HAVAL, like diablo2oo2’s previous crackmes.

• The bytestream from the HAVAL hash function is converted into a string, which is the “ID” shown before.
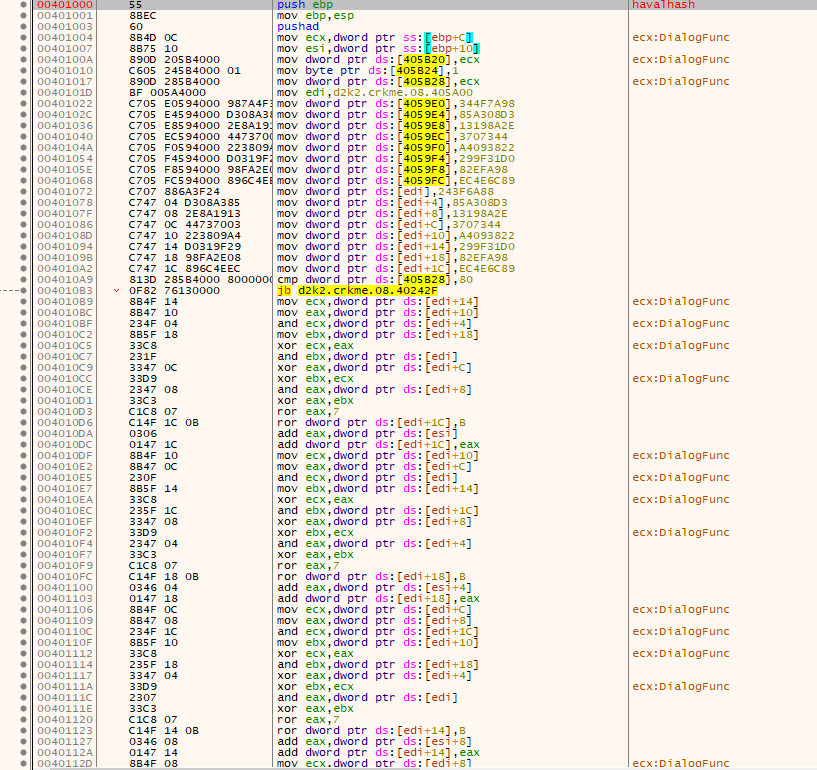
• The contents of the HAVAL hash bytestream are used to determine offsets in a table which is later used in the crackme with some bignum usage. Some ROR and ROL opcodes which are used in the main checking stage are modified here, so the crackme has self-modifying code.

In C, this can be shown as the following

    Register EB, EA, ED;
	uint8_t bignum_tabloff1;
	uint8_t bignum_tabloff2;
	uint8_t rotr_var = 8;
	uint8_t rotl_var = 0x10;
	uint32_t* hash_ptr = haval_hash;

	EA.ex = *hash_ptr;
	EA.ex = _rotr(EA.ex, 8);
	EB.ex = *(uint32_t*)(hash_ptr + 1);
	EA.ex = _rotl(EA.ex, 4);
	EA.ex ^= EB.ex;
	ED.ex = EA.ex % 0x80;
	EA.ex = EA.ex / 0x80;
	bignum_tabloff1 = ED.ex;
	ED.ex = EA.ex % 0x80;
	EA.ex = EA.ex / 0x80;
	bignum_tabloff2 = ED.ex;

	for(int i=0;i<computer_namelen;i++)
	{
		rotr_var += ED.b.lo;
		rotl_var -= EA.b.lo;
	}

• The table used is byteswapped.

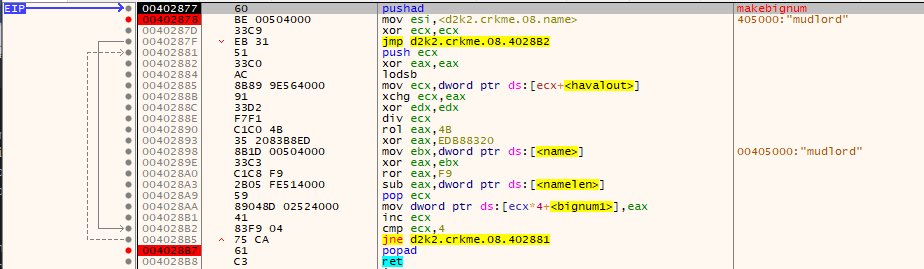
In the main checkroutine, in “makebignum” the following happens:

In C this can be rewritten as the following:

	uint32_t* ser_ptr = serialhash;
	for (int i = 0; i < 4; i++)
	{
		uint8_t chr = entered_name[i];
		uint32_t hash_frag = *(uint32_t*)((uint8_t*)hash_ptr + i);
		uint32_t name_frag = *(uint32_t*)entered_name;
		hash_frag = hash_frag / chr;
		hash_frag = _rotl(hash_frag, rotl_var);
		hash_frag ^= 0xEDB88320;
		hash_frag ^= name_frag;
		hash_frag = _rotr(hash_frag, rotr_var);
		hash_frag -= entered_namelen;
		*(uint32_t*)(ser_ptr + i) = hash_frag;
	}

This code is used to make a bignum which is used in this routine

In this routine, I have labeled the various variables used. In this case, 2 bignums are made from data selected from the table which was byteswapped earlier. They are then multiplied into another bignum which then used in the RSA operation down the track.

The RSA problem.

RSA (a form of public key encryption) works with the following formula:

serial = input ^ D mod N for decryption

and

outputserial = enteredserial ^ exponent mod N for encryption

The problem is: How do we determine D if we only have P, Q, and E, which in our case is the 2 bignums made from the bignum prime table and the RSA exponent?

The key to this is a mathematical operation called “Modular multiplicative inverse”. It is a process in which D can be determined if we only have P, Q, and E!

The maths behind this are the following: D=E^(-1) mod ((P-1)*(Q-1)).

This can be implemented in C using mbedtls’s bignum library as follows:

	mbedtls_mpi P, Q, E, N,temp_N, D,serialhash_bn, serial;
	
	mbedtls_mpi_init(&P); mbedtls_mpi_init(&Q); mbedtls_mpi_init(&E);
	mbedtls_mpi_init(&N); mbedtls_mpi_init(&D); mbedtls_mpi_init(&serial);
	mbedtls_mpi_init(&serialhash_bn); mbedtls_mpi_init(&temp_N);
	mbedtls_mpi_read_binary(&P, &bignum_tabl[bignum_tabloff1],8);
	mbedtls_mpi_read_binary(&Q, &bignum_tabl[bignum_tabloff2],8);
	mbedtls_mpi_read_binary(&serialhash_bn, serialhash, 8);
	mbedtls_mpi_read_string(&E, 16, "10001");
	//to get D we need  D=E^(-1) mod ((P-1)*(Q-1))
	//get N first
	mbedtls_mpi_mul_mpi(&N, &P, &Q);
	//so decrement P and Q :)
	mbedtls_mpi_sub_int(&P, &P,1);
	mbedtls_mpi_sub_int(&Q, &Q,1);
	//get temp_N which is ((P-1)*(Q-1))
	mbedtls_mpi_mul_mpi(&temp_N, &P, &Q);
	//to get D we need modular inverse!
	mbedtls_mpi_inv_mod(&D,&E,&temp_N);
	//we got D! :D now we use regular RSA operation (serial = input ^ D mod N)
	mbedtls_mpi_exp_mod(&serial, &serialhash_bn,&D, &N,NULL);

	TCHAR hash_ascii[0x80] = { 0 };
	int len;
	mbedtls_mpi_write_string(&serial, 16,hash_ascii, 0x80, &len);

	mbedtls_mpi_free(&P); mbedtls_mpi_free(&Q); mbedtls_mpi_free(&E);
	mbedtls_mpi_free(&N); mbedtls_mpi_free(&D); mbedtls_mpi_free(&serial);
	mbedtls_mpi_free(&serialhash_bn); mbedtls_mpi_free(&temp_N);

Keygen source code.

Source code to the keygen is here.

The accompanying x86 assembly for the keygen is here.

MSVC2019 is used to compile. It should compile out of the box, however you need to include the bignum library source files (included), into the solution.

Feel free to use the template for your own crackme keygens.